Elementos de los triángulos
Triángulo
Es la porción de plano limitada por tres rectas que se cortan dos a dos.
Es la porción de plano limitada por tres rectas que se cortan dos a dos.
Un triángulo tiene:
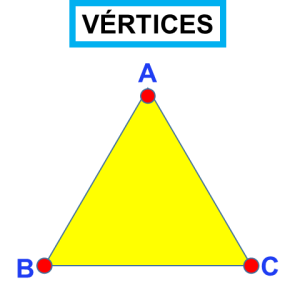
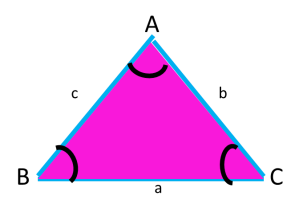
Tres vértices. Son los puntos de intersección del triángulo. Se nombran con letras mayúsculas.
Tres vértices. Son los puntos de intersección del triángulo. Se nombran con letras mayúsculas.
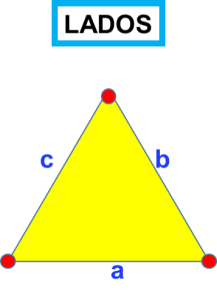
Tres lados. Son los segmentos determinados y se nombran con letras minúsculas.
Tres ángulos. Los lados forman los ángulos interiores que se nombran por las letras de los vértices.
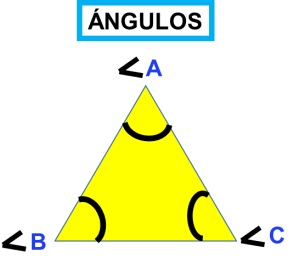

El lado opuesto a un ángulo, se nombra con la misma letra, pero minúscula.
Clasificación de los triángulos
Ver vídeo
Atendiendo a la medida de sus lados, los triángulos se dividen en:
a) Triángulo equilátero. Es el que tiene sus tres lados y sus tres ángulos iguales.
Atendiendo a la medida de sus lados, los triángulos se dividen en:
a) Triángulo equilátero. Es el que tiene sus tres lados y sus tres ángulos iguales.
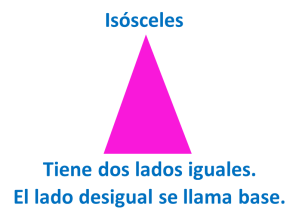
b) Triángulo isósceles. Es el que tiene dos lados iguales y los ángulos opuestos a dichos lados, también son iguales.
c) Triángulo escaleno. Es el que tiene sus tres lados y sus tres ángulos diferentes.

Atendiendo a los ángulos pueden ser:
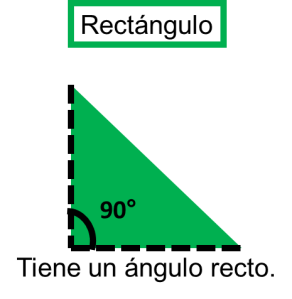
a) Triángulo rectángulo. Es el que tiene un ángulo recto. Sus lados reciben nombres especiales:
Catetos. Son los lados que forman el ángulo recto.
Hipotenusa. Es el lado opuesto al ángulo recto.
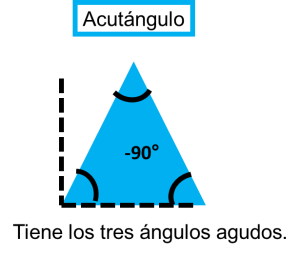
b) Triángulo acutángulo. Es el que tiene los tres ángulos agudos.
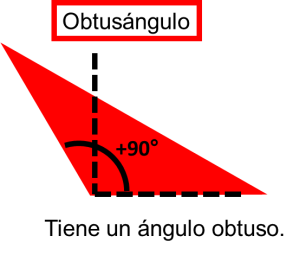
c) Triángulo obtusángulo. Es el que tiene un ángulo obtuso.
Cuando conoces la longitud del perímetro de un triángulo, puedes darle el valor a cada uno de sus lados sabiendo que la suma de los tres valores debe ser igual al perímetro dado.
Ejemplo: Si te dicen que el perímetro de un triángulo es igual a 15 cm, que obtengas la medida de cada uno de los lados del triángulo, lo primero que tienes que hacer es decidir qué tipo de triángulo será, y considerando las características de ese triángulo, dividir la longitud entre sus lados.
Ejemplo: Si te dicen que el perímetro de un triángulo es igual a 15 cm, que obtengas la medida de cada uno de los lados del triángulo, lo primero que tienes que hacer es decidir qué tipo de triángulo será, y considerando las características de ese triángulo, dividir la longitud entre sus lados.
Rectas y puntos notables en los triángulos
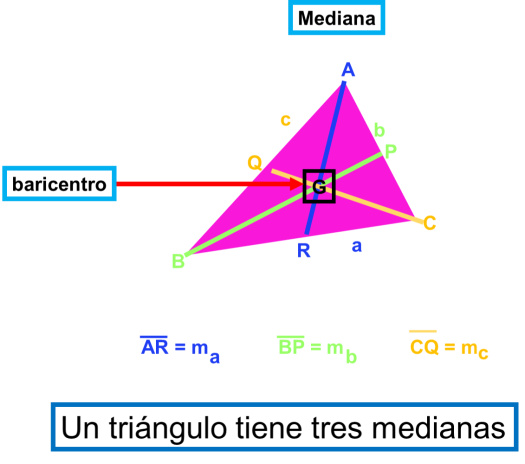
a)Mediana. Es el segmento trazado desde un vértice hasta el punto medio del lado opuesto.
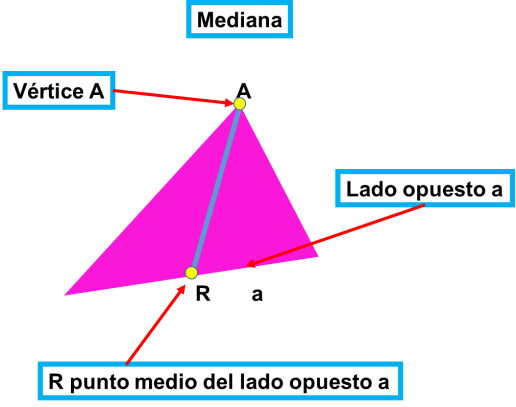
Hay tres medianas que corresponden una a cada lado. Se les designa con la letra “m” y un subíndice que indica el lado.
El punto donde se cortan las tres medianas se llama baricentro.
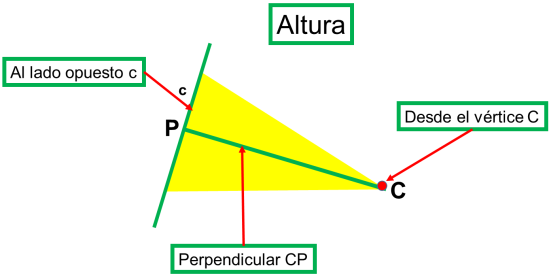
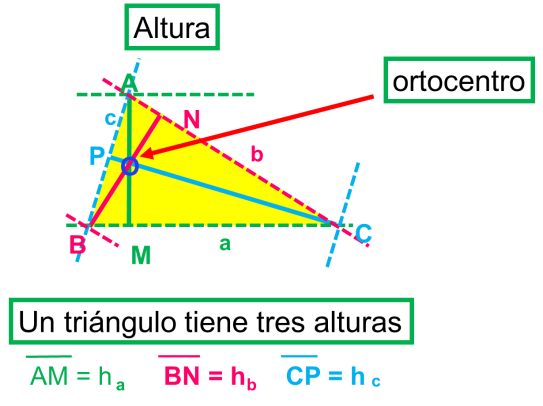
b) Altura. Es la perpendicular trazada desde un vértice, al lado opuesto o a su prolongación.
Hay tres alturas, una correspondiente a cada lado. Se designan con la letra “h” y un subíndice que indica el lado. El punto donde intersectan las tres alturas se llama ortocentro.
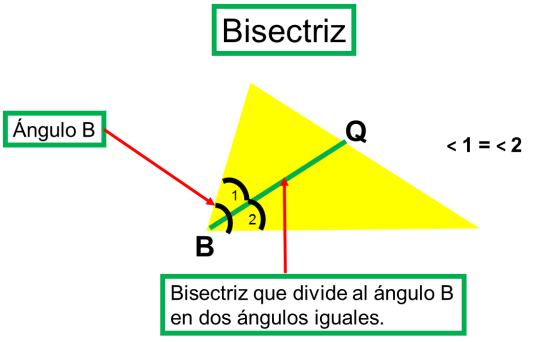
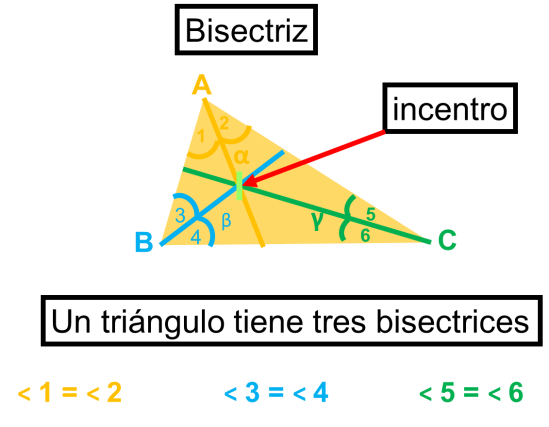
c) Bisectriz. Es la recta que corresponde a la bisectriz de un ángulo interior (divide al ángulo en dos ángulos iguales).
Hay tres bisectrices, una para cada ángulo; se nombran generalmente con las letras griegas alfa, beta y gamma.
El punto donde concurren las tres bisectrices se llama incentro.
El punto donde concurren las tres bisectrices se llama incentro.
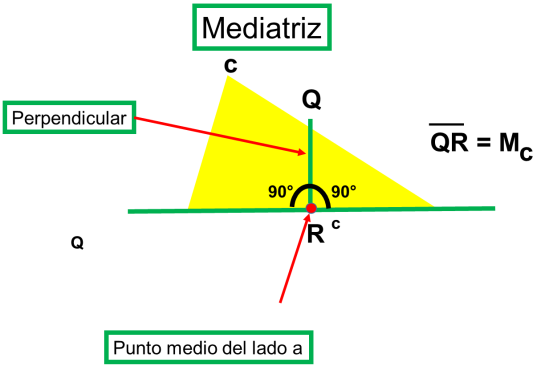
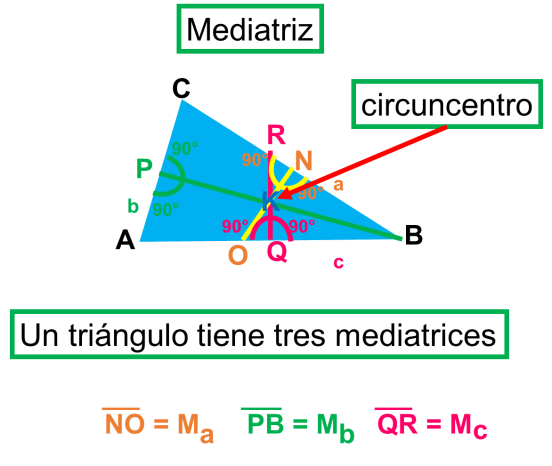
d) Mediatriz. Es la perpendicular en el punto medio de cada lado.
Hay tres mediatrices que se denominan con la letra “M” y un subíndice que indica el lado. El punto de intersección de las tres mediatrices se llama circuncentro.
La suma de los tres ángulos interiores de un triángulo es igual a 180°.
Simetría y diagonales
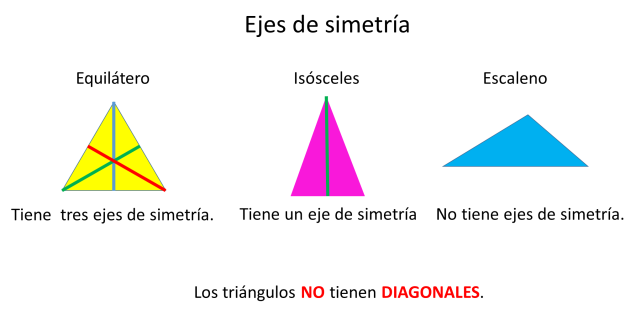
De acuerdo a la forma del triángulo, varía la cantidad de ejes de simetría.
Los triángulos no tienen diagonales,ya que como recordarás, una diagonal es el segmento de recta que une dos vértices no consecutivos.
Los triángulos no tienen diagonales,ya que como recordarás, una diagonal es el segmento de recta que une dos vértices no consecutivos.



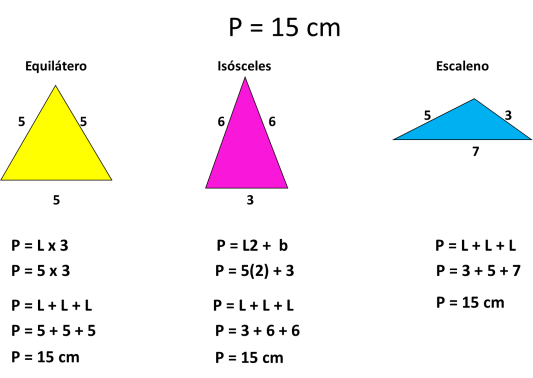





No hay comentarios:
Publicar un comentario