pág 57: 1, 2, 3, 4. 5VOL
Qué son los números primos?
Los números primos son aquellos que solo son divisibles entre ellos mismos y el 1, es decir, que si intentamos dividirlos por cualquier otro número, el resultado no es entero. Dicho de otra forma, si haces la división por cualquier número que no sea 1 o él mismo, se obtiene un resto distinto de cero.
Tabla de números primos hasta el 100
Vamos a construir la tabla de todos los números primos que existen hasta el 100.
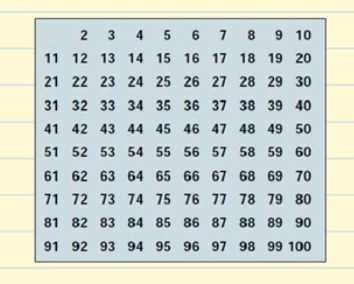
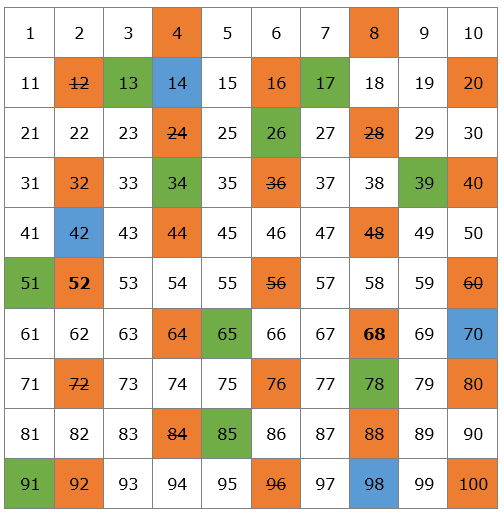
Vamos a empezar con el 2. El 2 es un número primo pero todos lo múltiplos de 2 serán números compuestos, ya que serán divisibles entre 2. Tachamos de nuestra tabla todos los múltiplos de 2.
El siguiente número primo es el 3, por lo tanto podemos tachar todos los múltiplos de 3, ya que serán números compuestos.
El siguiente número primo es el 5, por lo que tachamos todos los múltiplos de 5.
El siguiente número primo es el 7, así que tachamos todos los múltiplos de 7.
El siguiente número primo es el 11, por lo que tachamos todos los múltiplos de 11, que son el 22, 33, 44, 55, 66, 77, 88, y el 99. Todos estos ya habían sido tachados con anterioridad, por lo que ya hemos terminado de tachar todos los números compuestos de nuestra tabla.
Esta es nuestra lista de números primos del 1 al 100. No es necesario que te los aprendas de memoria, pero si que te acuerdes de los más pequeños, como el 2, 3, 5, 7, 11, 13.
¿Cuántos números primos hay?
El matemático griego Eratóstenes (siglo III a.C.) ideó una manera rápida de obtener todos los números primos hasta uno concreto. Se trata de un procedimiento denominado Criba de Eratóstenes.
Fíjate que entre 1 y 100 hay 25 números primos. ¿Cuántos números primos habrá en total? Pues se conoce desde la antigüedad que son infinitos, por eso resulta imposible dar una lista de todos ellos. Como Euclides, que fue el primero en demostrar que eran infinitos en el siglo IV a.C, no conocía el concepto de infinito decía que “los números primos son más que cualquier multitud fijada de ellos” esto es, que si imaginas que son 100, son más, y si imaginas que son un millón, pues también son más.
Tabla de números primos desde el 100 hasta el 1.000
Aquí van los números primos desde el 100 hasta el 1.000.
Perdona que no te los ponga todos, porque ya sabes que son infinitos. 
Problemas de números primos
Para que lo entiendas mejor, vamos a explicarlo con un problema.
Sara tiene 6 caramelos y los quiere repartir, pero no sabe muy bien entre cuántas personas puede hacerlo para que a todas las personas les toquen los mismos caramelos y no sobre ninguno. ¿De cuántas formas puede hacerlo?
Aquí están Sara y sus 6 caramelos:
¿Cómo podemos dividirlos?
Lo primero y más fácil es dárselos todos a una persona, es decir, dividirlo entre 1. Con lo que a esa persona le tocarían ¡6 caramelos!
La siguiente posibilidad es repartirlos entre 2 personas. Como 6 entre 2 es 3, ¡tocarían 3 caramelos a cada uno!
Vamos con el siguiente número, el 3. Si dividimos 6 caramelos entre 3 personas también tenemos una división exacta y tocan a 2 caramelos cada persona:
Seguimos con los números. No tenemos divisiones exactas entre 4 y 5 pero sí entre 6.
Como 6 entre 6 es 1, podemos dar caramelos a 6 niños, dándole un caramelos a cada uno.
Vamos a recopilar información. Tenemos que 6 caramelos los podemos repartir (siendo exacto el reparto) entre 1, 2, 3 y 6 personas. Es decir, el número 6 lo podemos dividir, de forma que el resto sea 0, entre 1, 2, 3 y 6. Estos números se llaman divisores del 6.
Probemos con otro número. Por ejemplo el 7.
Ahora Sara tiene 7 caramelos y los quiere repartir, pero no sabe muy bien entre cuántas personas puede hacerlo para que a todas las personas les toquen los mismos caramelos y no sobre ninguno. ¿De cuántas formas puede hacerlo?
¡Qué suerte tiene Sergio que se ha quedado todos los caramelos!
¿Hay más formas de hacerlo? El 7 no lo podemos dividir ni entre 2, ni entre 3, ni entre 4, ni entre 5, ni entre 6… ¡así que sólo nos queda el 7!
Sara puede repartir los caramelos entre 7 personas dándoles uno a cada uno:
Así que 7 sólo se puede dividir entre 1 y entre 7, sus únicos divisores son el 1 y el 7. A este tipo de números los llamamos números primos.
¿Hay más números primos? ¡Claro que sí! Busquemos alguno más:
- ¿El 4? ¡No! Porque sus divisores son 1, 2 y 4.
- ¿El 5? ¡Sí! Porque sus divisores son 1 y 5.
- ¿El 8? ¡No! Porque sus divisores son 1, 2, 4 y 8.
En resumen, un número es primo si sólo tiene dos divisores: el 1 y él mismo.
¡Ya puedes buscar un montón de números primos!
¿Cómo saber si un número es primo?
¡Presta mucha atención! Vamos a darte un truco para saber si un número es primo o no, sin tener que buscar sus divisores, sino de una manera mucho más lúdica y que a la vez también nos proporcionará sus divisores (si los tiene).
Elegimos un número al azar, por ejemplo el 16.
Para comprobar si es un número primo o no, vamos a utilizar una tabla, muy parecida a las tarjetas Montessori para multiplicar. Y cogemos tantas bolitas como el número que hemos escogido, en este caso 16 bolas.
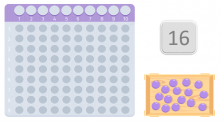
Una vez tenemos la tabla y las bolitas, debemos colocarlas en la tabla empezando por el primer hueco, intentando formar un rectángulo. Los números que delimiten el rectángulo serán divisores de ese número.
En caso de que solo consigamos formar un rectángulo con el mismo número que estamos utilizando y el 1, se tratará de un número primo.
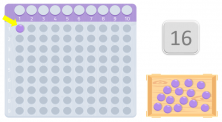
Por ejemplo, en este caso, colocamos 8 bolitas en la primera fila y 8 más en la segunda. Como podéis ver, hemos formado un rectángulo, y vemos que tanto el 8 como el 2 son divisores del número 16. Por lo tanto, el número 16 no es un número primo. Porque, como ya sabemos, los números primos son aquellos que solo son divisibles entre ellos mismos y el 1.
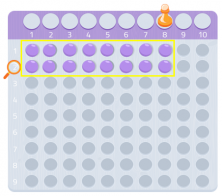
Probemos ahora con otro número, el 7 por ejemplo.
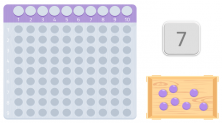
Como podemos ver, no conseguimos hacer un rectángulo completo, nos faltaría una bolita. Al no haber podido formar un rectángulo podemos afirmar que el número 7 no tiene divisores, exceptuando él mismo y el 1, como vemos en la siguiente imagen.
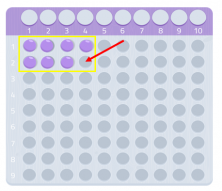
Por lo tanto, ¡el número 7 es un número primo!
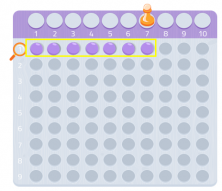
Prueba con cualquier otro número, ¡verás como funciona! Puedes utilizar un cuaderno de cuadros y buscar los rectángulos posibles usando esa cantidad de cuadraditos.
¿El 1 es primo?
Hay gente que cree que sí, porque dicen que 1 solo se puede dividir entre 1 y entre sí mismo, pero en matemáticas se ha descartado el número uno como primo por tener un solo divisor. De hecho, se utiliza el criterio de “un número entero positivo es primo si tiene exactamente dos divisores positivos” para excluir al uno de la lista de números primos. No es porque le tengamos manía, pero si el número uno se considerase primo habría que decir de forma diferente muchas propiedades matemáticas.
Entonces, ¿el 1 es compuesto?
Pues tampoco, ya que no se puede poner como producto de primos. El número 1 no es ni primo ni compuesto. Y, antes de que vayas a preguntar, el cero tampoco es primo ni compuesto, pero esto es porque todas las consideraciones que estamos haciendo son para números positivos, o sea, mayores que cero.
Para qué sirven los números primos. Ejemplos en la naturaleza
Los números primos son la clave de la aritmética, a continuación verás un ejemplo que demuestra su importancia, no solo en el cálculo aritmético sino en la naturaleza.
¿Qué significa que los números primos son la clave de la aritmética?
Esto es así porque cualquier número está formado por el producto único de una serie de estos números.
Se cree que se llevan estudiando desde hace unos 20.000 años, cuando algún antepasado nuestro grabó en el Hueso de Ishango una cuaterna de números primos (11, 13, 17 y 19). Por si esto fuera una coincidencia, se confirma que los antiguos egipcios ya trabajaban con ellos hace 4.000 años.
Además, la naturaleza los conoce muy bien y algunas especies han sido capaces de descubrirlos a lo largo de su evolución y aprovecharse de ellos para su supervivencia.
Me estoy refiriendo a varias especies de cigarras como la Magicicada septendecium, que vive en Norteamérica. Estas especies de cigarras han establecido su ciclo de reproducción en torno a los 13 o 17 años, no 12, ni 14, ni 15, ni 16 o 18, exactamente cada 13 o 17 años. Esto les permite evitar a depredadores que tengan ciclos reproductivos también periódicos; imaginemos un depredador con un ciclo de 4 años.
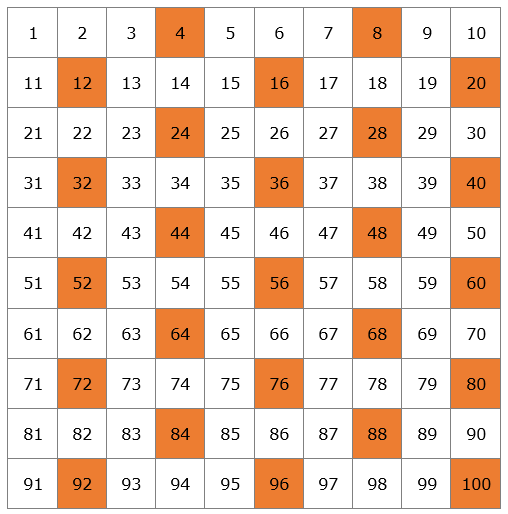Si el ciclo vital de la cigarra fuese de 12 años o 14, coincidiría con su depredador muy frecuentemente, mucho más que si fuese de 13 o 17 años. Exactamente 2 veces en 100 años, mientras que, del otro modo, coincidirían en 11 ciclos, comprometiendo el desarrollo de la especie.
En los números primos se basa la seguridad de las comunicaciones electrónicas. Cada mensaje encriptado que se manda por internet (redes de mensajería, compras o banca electrónica) lleva asociado un número grande, que es muy difícil de saber si es primo o no. El receptor tiene uno de sus divisores y por eso puede desencriptarlo. Así que los números primos son fundamentales para tener privacidad en nuestras comunicaciones.
¿Qué son los números compuestos?
Son aquellos números que además de ser divisibles por ellos mismos y la unidad, también son divisibles por otros números.
Vamos a ver un ejemplo de número primo y un ejemplo de número compuesto.
El 11 se puede escribir como la multiplicación de 1 x 11, pero no se puede escribir como ninguna otra multiplicación de números naturales. Solo tiene como divisores el 1 y el 11, por lo tanto es un número primo.
El 12 se puede escribir como la multiplicación de 1 x 12, y también se puede escribir como la multiplicación de 3 x 4, y de 2 x 6. Como 12 es divisible por más números de 1 y el mismo, 12 es un número compuesto.
Divisores de un número
El divisor de un número es el valor que divide al número en partes exactas, es decir, que el resto sea 0.
Por ejemplo, vamos a calcular los divisores de 24.
Empezamos dividiendo entre los números más pequeños, desde el 1.
- 24 / 1 = 24. Tanto 1 como 24 son sus divisores.
- 24 / 2 = 12. 2 y 12 son sus divisores.
- 24 / 3 = 8. 3 y 8 son sus divisores.
- 24 / 4 = 6. 4 y 6 son sus divisores.
- 24 / 5 = 4. No es una división exacta ya que el resto es 4, por lo tanto 5 no es un divisor.
El siguiente número es el 6, pero como ya tenemos el 6 como divisor de 24, ya hemos terminado de calcular los divisores de 24.ág
Qué son los números primos?
Los números primos son aquellos que solo son divisibles entre ellos mismos y el 1, es decir, que si intentamos dividirlos por cualquier otro número, el resultado no es entero. Dicho de otra forma, si haces la división por cualquier número que no sea 1 o él mismo, se obtiene un resto distinto de cero.
Tabla de números primos hasta el 100
Vamos a construir la tabla de todos los números primos que existen hasta el 100.
Vamos a empezar con el 2. El 2 es un número primo pero todos lo múltiplos de 2 serán números compuestos, ya que serán divisibles entre 2. Tachamos de nuestra tabla todos los múltiplos de 2.
El siguiente número primo es el 3, por lo tanto podemos tachar todos los múltiplos de 3, ya que serán números compuestos.
El siguiente número primo es el 5, por lo que tachamos todos los múltiplos de 5.
El siguiente número primo es el 7, así que tachamos todos los múltiplos de 7.
El siguiente número primo es el 11, por lo que tachamos todos los múltiplos de 11, que son el 22, 33, 44, 55, 66, 77, 88, y el 99. Todos estos ya habían sido tachados con anterioridad, por lo que ya hemos terminado de tachar todos los números compuestos de nuestra tabla.
Esta es nuestra lista de números primos del 1 al 100. No es necesario que te los aprendas de memoria, pero si que te acuerdes de los más pequeños, como el 2, 3, 5, 7, 11, 13.
¿Cuántos números primos hay?
El matemático griego Eratóstenes (siglo III a.C.) ideó una manera rápida de obtener todos los números primos hasta uno concreto. Se trata de un procedimiento denominado Criba de Eratóstenes.
Fíjate que entre 1 y 100 hay 25 números primos. ¿Cuántos números primos habrá en total? Pues se conoce desde la antigüedad que son infinitos, por eso resulta imposible dar una lista de todos ellos. Como Euclides, que fue el primero en demostrar que eran infinitos en el siglo IV a.C, no conocía el concepto de infinito decía que “los números primos son más que cualquier multitud fijada de ellos” esto es, que si imaginas que son 100, son más, y si imaginas que son un millón, pues también son más.
Tabla de números primos desde el 100 hasta el 1.000
Aquí van los números primos desde el 100 hasta el 1.000.
Perdona que no te los ponga todos, porque ya sabes que son infinitos.
Problemas de números primos
Para que lo entiendas mejor, vamos a explicarlo con un problema.
Sara tiene 6 caramelos y los quiere repartir, pero no sabe muy bien entre cuántas personas puede hacerlo para que a todas las personas les toquen los mismos caramelos y no sobre ninguno. ¿De cuántas formas puede hacerlo?
Aquí están Sara y sus 6 caramelos:
¿Cómo podemos dividirlos?
Lo primero y más fácil es dárselos todos a una persona, es decir, dividirlo entre 1. Con lo que a esa persona le tocarían ¡6 caramelos!
La siguiente posibilidad es repartirlos entre 2 personas. Como 6 entre 2 es 3, ¡tocarían 3 caramelos a cada uno!
Vamos con el siguiente número, el 3. Si dividimos 6 caramelos entre 3 personas también tenemos una división exacta y tocan a 2 caramelos cada persona:
Seguimos con los números. No tenemos divisiones exactas entre 4 y 5 pero sí entre 6.
Como 6 entre 6 es 1, podemos dar caramelos a 6 niños, dándole un caramelos a cada uno.
Vamos a recopilar información. Tenemos que 6 caramelos los podemos repartir (siendo exacto el reparto) entre 1, 2, 3 y 6 personas. Es decir, el número 6 lo podemos dividir, de forma que el resto sea 0, entre 1, 2, 3 y 6. Estos números se llaman divisores del 6.
Probemos con otro número. Por ejemplo el 7.
Ahora Sara tiene 7 caramelos y los quiere repartir, pero no sabe muy bien entre cuántas personas puede hacerlo para que a todas las personas les toquen los mismos caramelos y no sobre ninguno. ¿De cuántas formas puede hacerlo?
¡Qué suerte tiene Sergio que se ha quedado todos los caramelos!
¿Hay más formas de hacerlo? El 7 no lo podemos dividir ni entre 2, ni entre 3, ni entre 4, ni entre 5, ni entre 6… ¡así que sólo nos queda el 7!
Sara puede repartir los caramelos entre 7 personas dándoles uno a cada uno:
Así que 7 sólo se puede dividir entre 1 y entre 7, sus únicos divisores son el 1 y el 7. A este tipo de números los llamamos números primos.
¿Hay más números primos? ¡Claro que sí! Busquemos alguno más:
- ¿El 4? ¡No! Porque sus divisores son 1, 2 y 4.
- ¿El 5? ¡Sí! Porque sus divisores son 1 y 5.
- ¿El 8? ¡No! Porque sus divisores son 1, 2, 4 y 8.
En resumen, un número es primo si sólo tiene dos divisores: el 1 y él mismo.
¡Ya puedes buscar un montón de números primos!
¿Cómo saber si un número es primo?
¡Presta mucha atención! Vamos a darte un truco para saber si un número es primo o no, sin tener que buscar sus divisores, sino de una manera mucho más lúdica y que a la vez también nos proporcionará sus divisores (si los tiene).
Elegimos un número al azar, por ejemplo el 16.
Para comprobar si es un número primo o no, vamos a utilizar una tabla, muy parecida a las tarjetas Montessori para multiplicar. Y cogemos tantas bolitas como el número que hemos escogido, en este caso 16 bolas.
Una vez tenemos la tabla y las bolitas, debemos colocarlas en la tabla empezando por el primer hueco, intentando formar un rectángulo. Los números que delimiten el rectángulo serán divisores de ese número.
En caso de que solo consigamos formar un rectángulo con el mismo número que estamos utilizando y el 1, se tratará de un número primo.
Por ejemplo, en este caso, colocamos 8 bolitas en la primera fila y 8 más en la segunda. Como podéis ver, hemos formado un rectángulo, y vemos que tanto el 8 como el 2 son divisores del número 16. Por lo tanto, el número 16 no es un número primo. Porque, como ya sabemos, los números primos son aquellos que solo son divisibles entre ellos mismos y el 1.
Probemos ahora con otro número, el 7 por ejemplo.
Como podemos ver, no conseguimos hacer un rectángulo completo, nos faltaría una bolita. Al no haber podido formar un rectángulo podemos afirmar que el número 7 no tiene divisores, exceptuando él mismo y el 1, como vemos en la siguiente imagen.
Por lo tanto, ¡el número 7 es un número primo!
Prueba con cualquier otro número, ¡verás como funciona! Puedes utilizar un cuaderno de cuadros y buscar los rectángulos posibles usando esa cantidad de cuadraditos.
¿El 1 es primo?
Hay gente que cree que sí, porque dicen que 1 solo se puede dividir entre 1 y entre sí mismo, pero en matemáticas se ha descartado el número uno como primo por tener un solo divisor. De hecho, se utiliza el criterio de “un número entero positivo es primo si tiene exactamente dos divisores positivos” para excluir al uno de la lista de números primos. No es porque le tengamos manía, pero si el número uno se considerase primo habría que decir de forma diferente muchas propiedades matemáticas.
Entonces, ¿el 1 es compuesto?
Pues tampoco, ya que no se puede poner como producto de primos. El número 1 no es ni primo ni compuesto. Y, antes de que vayas a preguntar, el cero tampoco es primo ni compuesto, pero esto es porque todas las consideraciones que estamos haciendo son para números positivos, o sea, mayores que cero.
Para qué sirven los números primos. Ejemplos en la naturaleza
Los números primos son la clave de la aritmética, a continuación verás un ejemplo que demuestra su importancia, no solo en el cálculo aritmético sino en la naturaleza.
¿Qué significa que los números primos son la clave de la aritmética?
Esto es así porque cualquier número está formado por el producto único de una serie de estos números.
Se cree que se llevan estudiando desde hace unos 20.000 años, cuando algún antepasado nuestro grabó en el Hueso de Ishango una cuaterna de números primos (11, 13, 17 y 19). Por si esto fuera una coincidencia, se confirma que los antiguos egipcios ya trabajaban con ellos hace 4.000 años.
Además, la naturaleza los conoce muy bien y algunas especies han sido capaces de descubrirlos a lo largo de su evolución y aprovecharse de ellos para su supervivencia.
Me estoy refiriendo a varias especies de cigarras como la Magicicada septendecium, que vive en Norteamérica. Estas especies de cigarras han establecido su ciclo de reproducción en torno a los 13 o 17 años, no 12, ni 14, ni 15, ni 16 o 18, exactamente cada 13 o 17 años. Esto les permite evitar a depredadores que tengan ciclos reproductivos también periódicos; imaginemos un depredador con un ciclo de 4 años.
Si el ciclo vital de la cigarra fuese de 12 años o 14, coincidiría con su depredador muy frecuentemente, mucho más que si fuese de 13 o 17 años. Exactamente 2 veces en 100 años, mientras que, del otro modo, coincidirían en 11 ciclos, comprometiendo el desarrollo de la especie.
En los números primos se basa la seguridad de las comunicaciones electrónicas. Cada mensaje encriptado que se manda por internet (redes de mensajería, compras o banca electrónica) lleva asociado un número grande, que es muy difícil de saber si es primo o no. El receptor tiene uno de sus divisores y por eso puede desencriptarlo. Así que los números primos son fundamentales para tener privacidad en nuestras comunicaciones.
¿Qué son los números compuestos?
Son aquellos números que además de ser divisibles por ellos mismos y la unidad, también son divisibles por otros números.
Vamos a ver un ejemplo de número primo y un ejemplo de número compuesto.
El 11 se puede escribir como la multiplicación de 1 x 11, pero no se puede escribir como ninguna otra multiplicación de números naturales. Solo tiene como divisores el 1 y el 11, por lo tanto es un número primo.
El 12 se puede escribir como la multiplicación de 1 x 12, y también se puede escribir como la multiplicación de 3 x 4, y de 2 x 6. Como 12 es divisible por más números de 1 y el mismo, 12 es un número compuesto.
Divisores de un número
El divisor de un número es el valor que divide al número en partes exactas, es decir, que el resto sea 0.
Por ejemplo, vamos a calcular los divisores de 24.
Empezamos dividiendo entre los números más pequeños, desde el 1.
- 24 / 1 = 24. Tanto 1 como 24 son sus divisores.
- 24 / 2 = 12. 2 y 12 son sus divisores.
- 24 / 3 = 8. 3 y 8 son sus divisores.
- 24 / 4 = 6. 4 y 6 son sus divisores.
- 24 / 5 = 4. No es una división exacta ya que el resto es 4, por lo tanto 5 no es un divisor.
El siguiente número es el 6, pero como ya tenemos el 6 como divisor de 24, ya hemos terminado de calcular los divisores de 24.ág
No hay comentarios:
Publicar un comentario