Empezamos tema, como siempre primero el índice 👆👆👆👆
Hoy hemos visto las fracciones equivalentes. Pág 108 y 109 : 1, 2, 3, 4 y 5. vol. Pensamiento.
Recordamos:
¿Qué son las fracciones equivalentes?
Fíjate en la siguiente imagen:
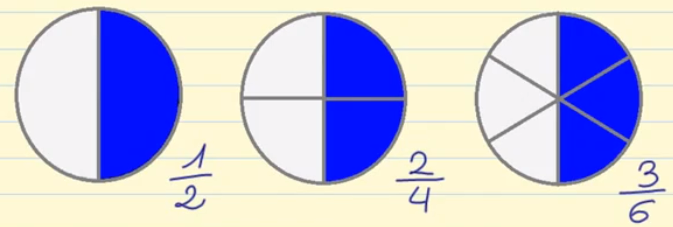
La primera figura está dividida en dos partes y hemos coloreado una de ellas. Por lo tanto, su fracción será 1/2.
La segunda figura la hemos dividido en 4 partes y hemos coloreado dos. Por lo tanto su fracción será 2/4.
Y la tercera figura la hemos dividido en 6 partes y hemos coloreado 3, por lo que su fracción será 3/6.
Si te fijas la parte coloreada en todas las figuras es la misma aunque las fracciones son diferentes: las tres fracciones dan el mismo resultado, son equivalentes.
¿Qué son las fracciones equivalentes?
Fracciones equivalentes son aquellas fracciones que representan la misma cantidad aunque el numerador y el denominador sean diferentes.
¿Cómo sabemos si dos fracciones son equivalentes?
Lo son si los productos del numerador de una y el denominador de la otra son iguales, es decir, productos cruzados.
Vamos a ver unos ejemplos:
Comprobemos si 2/5 y 4/10 son equivalentes.
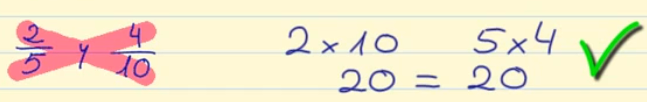
Para ello multiplicamos el numerados de una de las fracciones por el denominador de la otra.
2 x 10 = 20 5 x 4 = 20
Como el resultado es el mismo, podemos decir que 2/5 y 4/10 sí son fracciones equivalentes.
Ahora vamos a comprobar si 3/7 y 7/3 son fracciones equivalentes.
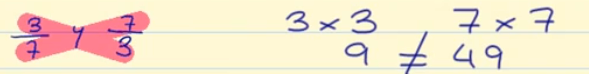
Para ello multiplicamos, como muestra la imagen:
3 x 3 = 9 7 x 7 = 49
Como el resultado no es el mismo, podemos decir que 3/7 y 7/3 no son equivalentes.
¿Cómo podemos calcular fracciones equivalentes?
Por amplificación
Multiplicando numerador y denominador por el mismo número.
Por ejemplo, partiendo de la fracción 1/3 y multiplicando el numerador y el denominador por el mismo número, podemos obtener diferentes fracciones equivalentes.
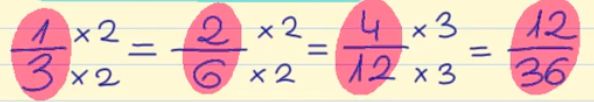
Si multiplicamos por 2: 1 x 2 = 2 3 x 2 = 6
por lo tanto la fracción 2/6 es equivalente a la fracción 1/3
Si volvemos a multiplicar por 2: 2 x 2 = 4 6 x 2 = 12
por lo tanto la fracción 4/12 es equivalente a 1/3 y a 2/6
Si ahora multiplicamos por 3: 4 x 3 = 12 12 x 3 = 36
por lo tanto 12/36 es una fracción equivalente a 1/3, a 2/6, y a 4/12
Vídeo tutorial sobre la amplificación
Echa un vistazo a este vídeo tutorial sobre la amplificación de fracciones.





No hay comentarios:
Publicar un comentario